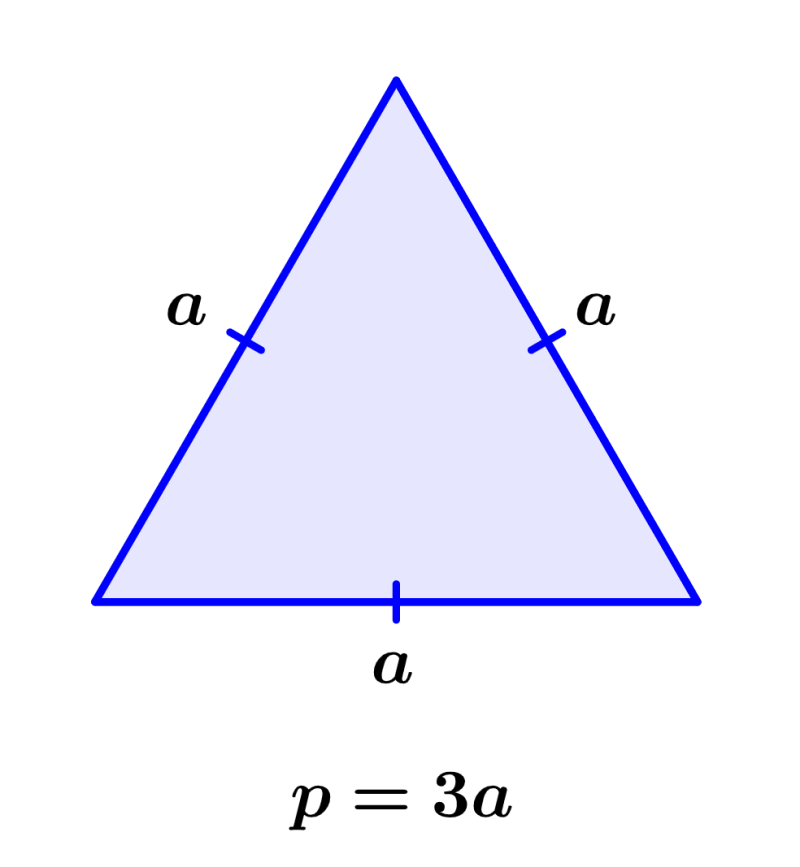
Triángulo equilátero
Un triángulo equilátero es un polígono de tres lados de igual longitud, sus ángulos internos también son iguales y son de 60°.
Nota: la suma de los ángulos internos de un triángulo es igual a 180°
Perímetro de un triángulo equilátero
Área de un triángulo equilátero
Si por alguna razón no conoces el valor de la altura (h) puedes utilizar la siguiente formula para calcular el área de un triángulo equilátero.
Construcción de un triángulo equilátero
- Una hoja de papel bond
- Un lápiz
- Un compás
- Y una regla
https://drive.google.com/file/d/1FOuWQukhMomt5UWe22k5puCNuP6zcKAB/view
Malla Curricular Área de Matemáticas
|
COMPETENCIAS |
INDICADORES DE
LOGRO |
CONTENIDOS |
|
Identifica
elementos comunes en patrones algebraicos y geométricos. |
Reconoce
figuras, relaciones, propiedades y medidas en diseños propuestos. |
Representación
de elementos básicos (punto, recta, rayo, plano, segmento, ángulo). |
|
Representación
de figuras abiertas, cerradas, cóncavas y convexas.
|
||
|
Terminología,
propiedades y trazo de rectas paralelas y perpendiculares |
||
|
Ángulos:
complementarios, suplementarios, alternos e internos |
||
|
Calcula
áreas y perímetros de polígonos regulares. |
Perímetro y área de polígonos regulares. |
Esta información la obtuve del CNB de Primero Básico, en él se establecen ciertas competencias, indicadores de logro y contenidos que nosotros como docentes debemos tener siempre presentes para impartir nuestras clases.
Libros de Guatematica
|
CONTENIDOS |
|
|
Sección1: Elementos básicos de línea y ángulo |
Punto,
recta, segmento, rayo y plano. Medida
de ángulos Ángulos
y su clasificación |
|
Sección 2: Ángulos y bisectriz |
Ángulos
complementarios y suplementarios Bisectriz
de un ángulo |
|
Sección 3: Propiedades y trazo de rectas paralelas,
perpendiculares y mediatriz. |
Líneas
paralelas y perpendiculares Construcción
de líneas paralelas Mediatriz
de un segmento Construcción
de mediatriz de un segmento |
|
Sección 4: Ángulos y líneas paralelas |
Ángulos
opuestos por el vértice Ángulos
correspondientes, alternos internos y alternos externos Ángulos
correspondientes y líneas paralelas Ángulos
alternos y líneas paralelas |
|
Sección 5: Polígonos |
Figuras
abiertas y cerradas Figuras
convexas y cóncavas Polígonos |
|
Sección 6: Cuadriláteros |
Clasificación
de cuadriláteros Perímetro
de cuadriláteros Área
de rectángulos y cuadrados Área
de paralelogramos Área
de rombos Área
de trapecios |
|
Sección 7: Triángulos |
Clasificación
de triángulos por sus lados Clasificación
de triángulos por sus ángulos Relación
entre los ángulos internos y externos de un triángulo Perímetro
de triángulos Área
de triángulos |
|
Sección 8: Propiedades y construcción de polígonos |
Construcción
de triángulos equiláteros Construcción
de cuadrados |
|
Sección 9: Simetría |
Simetría
axial Simetría radial |
Artículo de opinión
Los contenidos que se establecen en el CNB que
deberían aprender todos los estudiantes de primero básico sin importar de que
cultura son o si viven en el área rural o urbana; pertenecientes al sector
público o privado son los que se observan en la tabla 1, también aparece en
ella las competencias e indicadores de logro que los estudiantes deben lograr
para obtener un aprendizaje que se pueda comparar con el de otros países.
Pero lamentablemente los que realmente se
llegan a aprender no son ni la mitad de ellos, ya que el nivel de aprendizaje
que traen los estudiantes del nivel primario, es muy bajo y cuando ingresan al
nivel medio, ciclo básico, sus conocimientos no son muy fuertes, es decir no
tienen una base sustentable.
Y lo digo por experiencia propia, porque recordaba
que aún guardaba mi cuaderno de primero básico y buscando entre mis cuadernos,
lo encontré. Me acordaba solo de algunos temas vistos ese grado, pero de
geometría no recordaba nada. Y efectivamente al revisar mi cuaderno no encontré
nada sobre geometría, ningún tema visto, ningún ejercicio realizado, el
profesor no me enseño nada de geometría. Todo ese ciclo escolar aprendí sobre
aritmética y algebra temas como: sistemas de numeración, recta numérica,
jerarquía de operaciones, términos semejantes, clasificación de expresiones
algebraicas, suma y resta de polinomios.
Y creo que esto ocurre en la mayoría de
escuelas, institutos o colegios más aún si son del área rural los docentes se
enfocan en enseñar contenidos que “creen” que son más importantes que otros y
es por eso que los estudiantes aprenden solo lo básico, cuando en realidad
debería ser todo lo contrario, los docentes deberían enseñar todos los temas
que se establecen en el CNB, pero para que eso ocurra no solo depende del
docente sino también de los estudiantes.
Pero pueda ser que otros compañeros si
aprendieron sobre geometría en primero básico, esto es en base a mi
experiencia, también pueda ser que en el instituto donde estudie ahora sí los
estudiantes aprendan sobre geometría, ya que fue hace 10 años exactamente cuando
yo estuve en primero básico.
Ahora bien, en la tabla 2 aparecen los temas de
geometría que deben impartirse en primero básico, estos temas los obtuve del
libro de Guatemática que fue un proyecto de la Escuela de Formación de
Profesores de Enseñanza Media (EFPEM), Ministerio de Educación conjuntamente
con la Agencia de Cooperación Internacional de Japón (JICA).
La primera edición de este libro fue en el
2018, por lo que considero que donde han sido implementados los estudiantes
deben tener un mayor aprendizaje en cuando a la geometría porque en él aparecen
temas muy variados desde punto, recta, segmento pasando por los ángulos y su
clasificación, cuadriláteros, triángulos hasta llegar a simetría axial y
radial.
Este libro de texto está diseñado para que el
estudiante adquiera un aprendizaje acorde a su contexto, los problemas están
adaptados a situaciones de la vida cotidiana. Y sobre todo los temas están
acordes a los contenidos establecidos en el Currículum Nacional base de primero
básico.
Conclusiones
Uno de los aspectos que obstaculizan el
aprendizaje de la geometría puede ser retraso
en el aprendizaje de estudiantes de primaria, el no contar con libros de textos
adecuados al contexto del estudiante. Otro factor también pueda ser, que los
docentes no enseñan lo que deberían, es decir, lo establecido en el CNB.